Hyperfocal distance, much like the “Sunny 16 Rule,” is one of those things that has arguably lost some relevance in the age of digital photography; the sophisticated metering and auto focusing systems built into digital cameras have helped make life a little easier in some ways.

But there are times when some automated feature of your camera simply doesn’t come through for you, or times when you prefer to take away all your camera’s decision-making abilities and do it all for yourself. Then it’s good to know all those old school rules that you thought you would never have any use for.
One of those “old” photographic principles deemed useful by landscape photographers is that of hyperfocal distance which can be a confusing one for both beginners and experienced photographers, but is one that will help you with taking the sharpest images possible when it comes to photographing landscapes.
What Is Hyperfocal Distance?
To lay it out in simple terms, hyperfocal distance is the closest focusing distance at which your photos have the greatest depth of field, meaning a larger area or all areas from foreground to background remain in acceptably sharp focus.
In order to understand hyperfocal distance, you will need to have a good understanding of how changing aperture values in a lens and depth of field work and what factors affect the depth of field in an image. Some important points to keep in mind are:
- The wider the aperture opening is (small aperture values like f/1.4, f/1.8, f/2.8) the shallower the depth of field. The narrower the aperture opening is (large aperture values like f/7, f/11 and above), the deeper or greater the depth of field. So depending on your aperture values, you will have to focus either nearer (narrow aperture) or farther (wider aperture) away from your camera.

- When you focus on a foreground element, the background becomes out of focus and when you focus on a background element, the foreground becomes out of focus. In order to get the foreground and the background in focus, you will need to focus somewhere in between the foreground and background so you get all the regions in focus. This point of focus at which the foreground and background areas are in focus is called the hyperfocal distance.

- Focal length contributes to focusing distance for a scene. For lenses with smaller focal lengths (wide angle lenses), your hyperfocal distance will be closer to your lens (usually a few meters), whereas for lenses with longer focal lengths the hyperfocal distance will be very far from the lens.
- When focusing at hyperfocal distance, everything from half the hyperfocal distance up to infinity will appear sharp in the scene. For example, if you are using a wide particular lens and your hyperfocal distance is maybe 8 meters, then everything from 4 meters up to infinity will appear sharp.
Portrait photographers don’t typically see depth of field as something to overcome; a good portrait can be made from large apertures and small apertures alike. How much depth of field is present depends on how much of the subject the photographer wants to isolate.
Landscape photographers, however, face a different challenge. When shooting landscapes there are going to be numerous objects in a scene — there will be background elements and foreground elements. Furthermore, the distance between the background and foreground could very well be hundreds of feet. The goal is to get all this in focus. How, then, does one solve this depth of field riddle?

We know that depth of field increases with higher f-stops (f/16 creates more depth of field than f/4). We also know that depth of field increases as the camera focuses farther away.
So, imagine you are attempting to focus on a picturesque landscape scene using a 20mm lens set to f/11; you want to be sure that you’ve got the background as well as the foreground in sharp focus. You don’t want to run the risk of stopping the lens down too much and introducing diffraction, and you don’t want to guess on where to focus and end up with a blurry background.
What if there were a point at which you could focus so as to get as much of the scene as possible in focus? Something like that would be brilliant.
Luckily, such a thing exists. It is what is referred to as hyperfocal distance.
The hyperfocal distance is the point of focus that allows for maximum depth of field throughout a scene. Once you have focused on the hyperfocal point, everything from half the hyperfocal distance to infinity will be in focus.
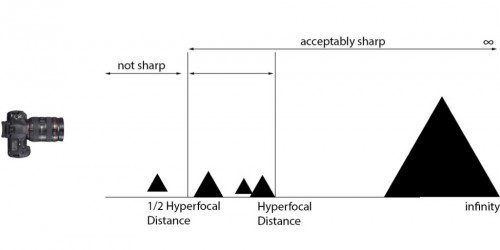
You may be wondering how exactly hyperfocal distance is determined; how do you know where that magical point is?
Calculating Hyperfocal Distance
In order to calculate hyperfocal distance, you need to know three things:
- Focal length – This will depend on what lens you’re using.
- Circle of confusion value – Commonly 0.03 and 0.02; depends on sensor type.
- F-stop – f/11 and f/13 are often regarded as optimal for landscape photography.
Next, use the following formula and do a little math (lengths and distances measured in mm):

Using the aforementioned scenario involving a 20mm lens at f/11 on a full-frame camera,
Hyperfocal distance = (20 x 20) / (0.03 x 11) = 400/0.33 = 1212.12mmSo, you get a hyperfocal distance of 1212 mm, or 1.2 meters (almost 4 feet). You should focus on an object that is approximately 1.2 meters away; everything from 0.6 meters (half the hyperfocal distance) away to infinity will be in focus.
And there you have it. It’s that simple (if you don’t forget to pack a calculator). Using hyperfocal distance will help you get landscape shots that are sharp front to back.
Check here if you want to find the circle of confusion value for your camera or use this online hyperfocal distance calculator. There is also a hyperfocal distance table by PhotoPills here.
When Should You Use Hyperfocal Distance?
Use hyperfocal distance when you want the entire scene to be acceptably sharp. For example, you may be photographing a scene that has elements in the foreground (not very close to the lens) and the background that you want to be in focus. By focusing at hyperfocal distance, you get these objects acceptably sharp in your image.

When Should You Avoid Using Hyperfocal Distance?
- When you do not have elements in the foreground that you want to be sharp, then you do not need to calculate or focus on hyperfocal distance. For example, when shooting from a higher vantage point, you do not need to calculate hyperfocal distance since you will not have elements closer to the lens that need to be in sharp focus.
- When you are focusing on a distant subject like a mountain peak or other subjects, you do not need to calculate hyperfocal distance since you do not have anything that you need to be in focus on the foreground.
- If you have elements that are very close to your camera, then avoid using hyperfocal distance because you cannot have objects that are a few inches away from your lens and objects at a distance to be in focus at the same time. In these situations, use either focus stacking technique or move further away from the foreground element.

Conclusion
Calculating hyperfocal distance is a complicated process where you consider the circle of confusion, focal length, aperture values, etc. If you are someone who is happy with focusing somewhere in between the foreground and the background to get a decently sharp image, and want to avoid these calculations, you can focus roughly one third into the scene to get all areas of the scene in focus. Remember to use narrow aperture values like f/11, f/16. Look for the lens’ sweet spot and use it for good quality and sharp images.
Further Resources on Landscape Photography Settings
If you have made it this far in learning hyperfocal distance, we are guessing you are really digging deeper into the workings of your camera and camera-craft in getting great landscape shots. We would recommend you continue that journey with our landscape photography settings article which is a little more general, but whose links include other more specialised settings for your image creation.





20 Comments
Jason,
I’d like to take a moment to thank you for all the wonderful articles of yours I have read here on lightstalking. They are all very informative and well written!
Thanks for the kind words, John. Glad you’re enjoying the articles!
For those days when you forget the calculator: a good general rule of thumb for this that actually works: focus 1/3 of the way into your shot, shoot with an aperture of around f11 or higher and you’ll get great landscape results.
I’ll keep this in mind. Thanks!
Thanks for the practical rule of thumb. Makes more sense to us that then a complicated formula.
jDevaun, this was a great article.
Andrew, I will keep 1/3 and f11 in mind.
Thanks guys.
I’ve had this explained to me several times, but not in such a simple and understandable way. As an avid lover of landscape photography, I appreciate your explanation. This is something I’ve wanted to understand for a long time.
You mentioned this calculation is for a full frame sensor. Is this the same calc for a sensor that is not full frame? I have a Canon EOS 70D and the sensor frame factor is 1.6. Do put the 1.6 factor in on the top line of the equation and multiple by the stated mm focal length on the lens?
@Kevin, No the crop factor is not used in the calculation
The canon 70D is not listed on the site mentionned in the article but since all other Canon crop sensor are listed at 0.019 my guess would be that it is too, So it would be:
Hyperfocal distance = (20 x 20) / (0.019 x 11) if you use a 20mm lens as in the above example the result would be 1914mm or somewhere around 6feet for your camera.
I know I am massively late to the party here but every time I try the calculation you mention above I get a completely different number. Id love to know what I am doing wrong because I am so determined work this out. Here’s is what I did…
20×20 = 400
0.019×11 = 0.209
So I’m guessing I have done something massively stupid here.
You’ve not made any mistake other than not to complete the equation:
20×20 = 400
0.019×11 = 0.209
So, divide 400 by 0.209 giving 1913.9mm (your focal length and circle of confusion are both in mm). Converting to feet, you get 6.28 feet.
It’s possibly a bit late to help you, but may help others
Very nice article! 🙂 Thanks J!
If I may a small trick I found helpful through my experience… If i don’t have a calculator, since its easy to know my start focal length of my lens e.g. 16mm (@f11) when I shoot landscape, then I figured out that through 35mm which is the maximum of my lens is for each 1mm I have to add 0,4ft all up to 35mm.
Of course this is a beautiful way for f11 (which for me is a great ap) and works like a charm in Fx. From that point I don’t even carry a calculator 🙂 1mm= +0.4ft
Thank you for such well-written article Jason.
I’ve been blindly using Hyperfocal Distance app and was oblivious to this simple formula. This provides ground to an otherwise useful but sketchy concept.
I would usually take a tentative composition of my shot, take note of a point that is at the edge of the bottom of that frame, then set the camera focus at 1/3 the distance from that point and the farthest object on the frame. Just my style, and it works fine for me.
Thanks Jason,
The trouble I have is not the calculation, but rather being accurate with my focus point. The new digital lenses only offer a limited amount m/ft settings and I find it difficult to guess when my hyperfocal distance farther than a simple distance like 1.2 meters. Any advice?
Very good. Years ago I worked out an empirical rule with results similar to yours but simpler for the lay person.
For f/11 on an FX Lens, square the focal length of the Lens in mm and drop the last two digits for hpd in feet. Done!
This is a field approximation that is accurate enough to meet any photographer’s ability to gauge the resulting distance.
To convert the result to other apertures, multiply/divide the result by 2 for 2 f-stops, by 1.4/0.7 for one f-stop.
Very well presented.
I think one more sentence to explain diffraction.
A lens is most sharp at f8.
Basically put most lenses are sharpest at f8, so opening up a great deal f 1.2 or closing down, f 22 will cause the light to bounce around or diffuse so your image is less sharp. The effect on good lenses is often minor but it is present. (there are times such as that the trade off is welcomed.)
And two things I miss from older cameras split screen focusing screens, and graphs on most if not all old lenses showing points where the hyperfocal distance would come into effect. It is rare to see on a lens today, I suppose because the cameras are often different and changing so fast.
Hello Jason, It is a very informative article. I have two questions:
1. Are we to measure the hyper focal distance using a measuring tape? It you are on the verge of a cliff that won’t be possible.
2. The central focusing point in the view finder is more powerful than the rest. So which focusing point is to be brought to the hyper focal point. So will the quality of the picture will be affected if focused using any of the other focus points?
Have a good day
Dilip
For me it is much easier looking on the lens. All that is needed is turn the focus ring infinity mark to the desired f/stop, calculations are not needed. The focus mark is in the center of the f/stop scale that reach left and right. First I choose the f/stop I desire, move the infinity mark to that f/stop. Under the focus mark is the hyperfocal distance.
Really nicely laid out and simple. I am going to try focusing half way to the subject and use f8 or smaller.